- Pubblicato il 3 apr 2023
- Ultima modifica 29 ago 2023
- 7 min
Cosa sono le porte logiche e a cosa servono
I circuiti dei dispositivi digitali che usiamo quotidianamente sono architetture ingegnose e complesse di porte logiche. Scopri cosa sono le porte logiche e come si realizza un circuito digitale con le porte logiche fondamentali.

Il funzionamento dei circuiti digitali si basa su segnali elettrici che assumono solo due valori di potenziale. A questi due valori la logica binaria associa i segnali logici di 0 e 1; l’elaborazione di segnali logici di tale semplicità è il compito di circuiti logici sempre più complessi, realizzati a partire da strutture logiche essenziali: le porte logiche.
In questa guida impareremo a familiarizzare con le porte logiche fondamentali e le relative funzioni logiche di somma, prodotto e negazione, scopriremo i componenti elettronici che le implementano e i circuiti integrati che le utilizzano, e infine vedremo come si arriva a progettare un circuito logico combinatorio a partire dalle porte logiche di base.
Cosa sono e come funzionano le porte logiche
Le porte logiche sono modelli matematici e circuitali degli operatori booleani, funzioni elementari di variabili che possono assumere solo il valore 0 o 1.
L’algebra booleana, ideata dal matematico inglese George Boole a metà ‘800, consente di descrivere un circuito digitale comunque complesso con una funzione logica espressa come combinazione di tre operatori booleani: la negazione logica NOT, il prodotto logico AND e la somma logica OR.
Le porte logiche fondamentali implementano questi tre operatori, come vedremo in seguito.
Come sono fatte le porte logiche
I componenti elettronici più adatti a implementare le porte logiche sono i transistor a effetto di campo Metallo-Ossido-Semiconduttore (MOSFET, abbreviati in MOS).
I MOS, nelle versioni PMOS ed NMOS, si comportano da interruttori a commutazione estremamente rapida, una caratteristica che li rende ideali per i circuiti in logica binaria.
L’esempio più noto è rappresentato dall’invertitore o porta logica NOT realizzato con la tecnologia CMOS (Complementary MOS) che impiega un PMOS e un NMOS in serie con i gate in comune, come nello schema che segue (il simbolo del PMOS presenta un pallino sul terminale di gate):
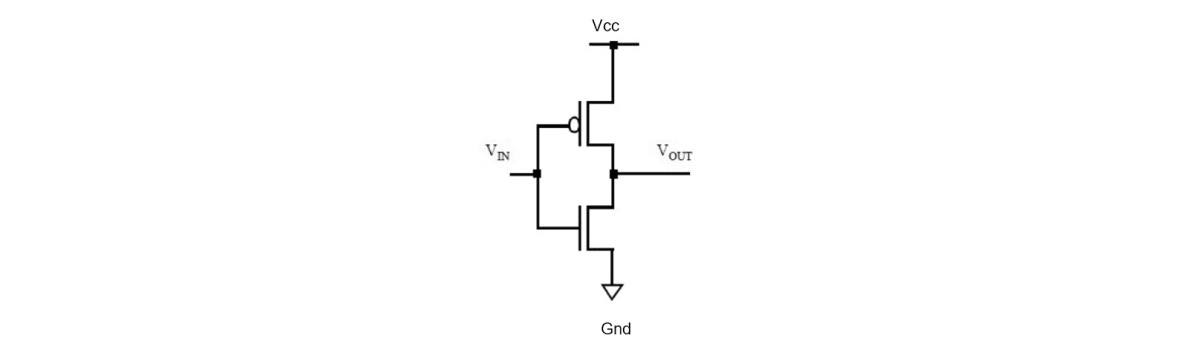
Il funzionamento da porta NOT o inverter del CMOS è molto efficace: se il segnale di ingresso ha un valore logico basso (Vin = 0 V), il transistor NMOS si comporta da interruttore aperto mentre il PMOS da interruttore chiuso, per cui l’uscita assume un valore logico alto (Vout = Vcc = 2,5 V). Diversamente, con l’ingresso al valore logico alto (Vin = 2,5 V), il PMOS è “aperto” e l’NMOS è “chiuso” e scarica Vout a Ground (0 V), per cui l’uscita è al valore logico basso.
In commercio le porte logiche sono presenti come circuiti integrati MOS (porte logiche multiple a 2 o più ingressi).

Tipi di porte logiche
Ogni porta logica può avere più variabili di ingresso ma presenta una sola variabile di uscita.
Le variabili di ingresso e di uscita sono di tipo digitale per cui è possibile inserire in una tabella detta tabella di verità tutte le possibili combinazioni che si possono verificare tra le variabili di ingresso.
Ma vediamo quali sono le porte logiche fondamentali da cui partire per realizzare porte logiche e circuiti logici (sia combinatori che sequenziali) di varia complessità.
Porte logiche NOT, AND e OR
La porta logica NOT implementa la funzione logica di negazione, ovvero restituisce in uscita il negato del valore logico dell’ingresso. Il simbolo circuitale della porta NOT (invertitore o inverter) è il seguente:

È immediato verificare che a tale funzione logica corrisponde la seguente tabella di verità:
A | OUT |
|---|---|
| 0 | 1 |
| 1 | 0 |
La porta logica AND implementa il prodotto logico, ovvero restituisce in uscita il valore logico alto se e solo se tutti gli ingressi sono al valore logico alto.
Il simbolo circuitale di una porta AND a due ingressi e la relativa tabella di verità sono i seguenti:

A | B | OUT |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La porta logica OR implementa la somma logica, ovvero restituisce in uscita il valore logico alto se almeno uno degli ingressi è al valore logico alto.
Il simbolo circuitale di una porta OR a due ingressi e la relativa tabella di verità sono i seguenti:

A | B | OUT |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Porte logiche NAND e NOR
La porta logica NAND implementa la funzione logica di negazione del prodotto logico, ovvero restituisce in uscita il negato del prodotto logico degli ingressi.
Il simbolo circuitale della porta NAND è il seguente:

Si verifica facilmente che alla funzione logica NAND corrisponde la seguente tabella di verità:
A | B | OUT |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La porta logica NOR implementa la funzione logica di negazione della somma logica, ovvero restituisce in uscita il negato della somma logica degli ingressi.
Il simbolo circuitale della porta NOR è il seguente:

Anche qui è facile costruire la tabella di verità a cui corrisponde la funzione logica NAND:
A | B | OUT |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Cos’è un circuito logico
Per quanto abbiamo visto finora, un circuito logico non è altro che una combinazione di più livelli di porte logiche per realizzare la vasta gamma di circuiti digitali combinatori e sequenziali esistenti, tra cui sommatori, traslatori logici, comparatori, PLA e memorie.
Vediamo come costruire un circuito logico e il circuito digitale combinatorio equivalente.
A cosa serve e come si costruisce un circuito logico
Supponiamo di avere tre ingressi A, B e C e una uscita OUT, e vogliamo realizzare un circuito in cui l’uscita è al valore logico alto quando abbiamo almeno due ingressi al valore logico alto, mentre in tutti gli altri casi l’uscita è al valore logico basso.
La tabella della verità corrispondente al requisito di progetto per il nostro circuito è la seguente:
A | B | C | OUT |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Ora dobbiamo ricavare la funzione logica equivalente alla tabella di verità.
A tale scopo, consideriamo tutte le combinazioni di A, B e C per le quali l’uscita vale 1. Affinché il prodotto logico ABC sia 1 (funzione logica AND), è necessario che tutti gli ingressi siano 1, per cui occorrerà prendere il valore negato di ogni ingresso che vale 0 in ognuna delle combinazioni per le quali OUT è al valore logico 1.
Fatto ciò, bisognerà effettuare la somma logica (funzione logica OR) dei prodotti logici ottenuti in precedenza, arrivando alla seguente espressione:
OUT = nA B C + A nB C + A B nC + A B C
dove nA, nB e nC indicano i negati dei valori logici di A, B e C rispettivamente.
Applicando le proprietà dell’algebra booleana possiamo semplificare la funzione logica che abbiamo ricavato. In particolare, considerando che:
- Si può aggiungere indefinitamente un termine logico a un’espressione senza che la funzione logica cambi;
- La somma logica di una variabile logica e della stessa variabile negata vale sempre 1;
aggiungiamo il prodotto logico ABC altre due volte:
OUT = nA B C + A nB C + A B nC + A B C+ A B C+ A B C
mettiamo in evidenza i termini comuni:
OUT = B C (A + nA) + A C (B + nB) + A B (C + nC)
e applichiamo la seconda proprietà sopra elencata (X + nX = 1), ottenendo in definitiva:
OUT = BC + AC + AB
La funzione logica finale è chiaramente una somma logica di prodotti logici, che si implementa con tre porte AND a due ingressi e due porte OR a due ingressi (oppure una sola porta OR a tre ingressi). Il circuito logico di progetto è, quindi, il seguente:
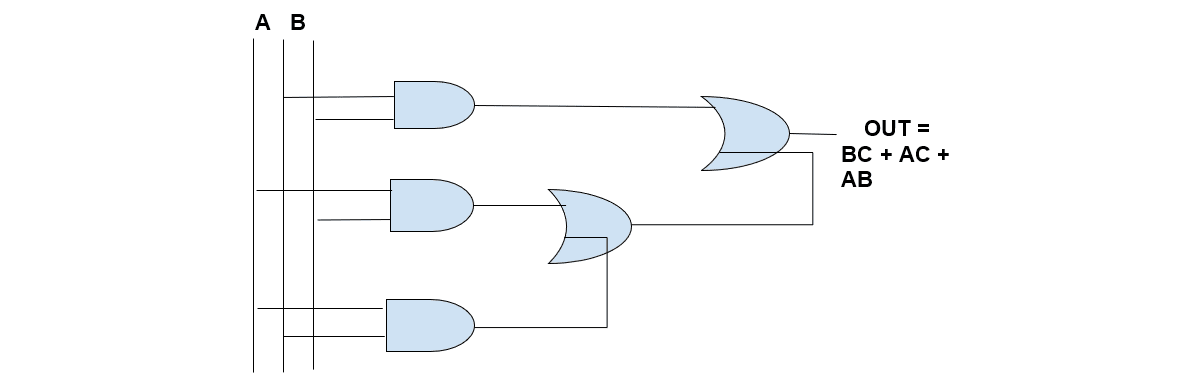
Si verifica facilmente che l'uscita OUT del circuito è al valore logico alto (1) quando almeno due tra gli ingressi A, B e C sono al valore logico alto, ed è al valore logico basso (0) per tutte le altre combinazioni dei valori logici di ingresso.
Concludendo
Questa guida ti ha fornito i concetti e le informazioni sul funzionamento e l’utilità delle porte logiche.
Visita la pagina dei circuiti integrati digitali di RS per scoprire la gamma completa di porte logiche e circuiti logici combinatori e sequenziali per tutte le tue esigenze “digitali”.
Prodotti Correlati
Gate logico OR Nexperia 5 Pin SC-74A
Gate logici famiglia 74LVC, Nexperia a bassa tensione, gruppo porta singola.
Array di circuiti logici programmabili
Memorie non volatili EPCx archiviano i dati di configurazione per array logici programmabili.
Sommatore binario CD74HC283E
Sommatori binari, comparatori di grandezza e uguaglianza, dispositivi di controllo di parità.
MC14504BDG Traslatore di livello logico
Dispositivi semiconduttori della famiglia CMOS, dotati di ampia gamma di tensioni d'esercizio: 3 a 18 V.



